Als je de voorwerpsafstanden nog een keer wilt bekijken, kun je hier klikken:
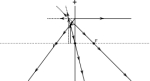
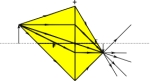
Voorwerpsafstanden



Samenvatting effect voorwerpsafstanden

Probeer zelf de samenvatting te bedenken ! Begrijp in ieder geval elke stap die gezet wordt !

We hebben de voorwerpsafstand kleiner gemaakt in stapjes en zagen wat er gebeurde met het beeld.
Als we dit in een tabel willen weergeven, dan moeten we kijken naar de verschillende waarden, die we zijn tegengekomen voor de voorwerpsafstand v, de beeldsafstand b, de voorwerpshoogte V, de beeldshoogte B en de vergroting.
De vergroting kunnen we op twee manieren berekenen: kijk nog maar eens naar het volgende plaatje. (Zie tekening)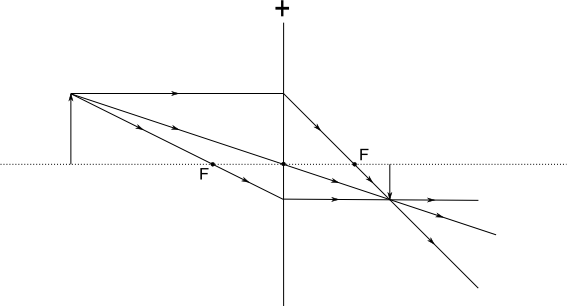


Vergroting N = beeldshoogte / voorwerpshoogte = B / V geeft 1 / 2 = 0,5.
Vergroting N = beeldsafstand / voorwerpsafstand = b / v geeft 3 / 6 = 0,5.
Let op het verschil tussen de grote en kleine letters !



Komt er uit die 2 manieren om de vergroting te berekenen nou altijd dezelfde waarde of je nou de ene of de andere manier gebruikt ?
Kijk maar eens naar het volgende plaatje, waarin 2 driehoeken aangegeven zijn.
De 2 driehoeken zijn gelijkvormig, want in beide driehoeken zijn er 3 hoeken even groot.
In beide driehoeken zit immers een hoek van 90º (linksonder en rechtsboven) en waar de driehoeken elkaar raken zijn twee overstaande hoeken, die aan elkaar gelijk zijn.
Omdat er al 2 hoeken even groot zijn, moet de 3e hoek ook even groot zijn, omdat in een driehoek alle hoeken bij elkaar altijd 180º zijn.
De driehoeken zijn dus gelijkvormig: dat wil zeggen, dat de ene driehoek in lengtes altijd een bepaalde factor groter is dan de andere driehoek.
En dat betekent dat als we de afstanden in de rechter driehoek delen door de bijbehorende afstanden in de linker driehoek we dus altijd hetzelfde getal krijgen.
Zo kunnen we dus B delen door V, maar ook b delen door v. In beide gevallen komt er dan dus de vergroting N uit !
We zouden zelfs de 2 schuine zijden door elkaar kunnen delen, maar die hebben helaas geen naam gekregen..
Er geldt dus: N = B / V ( = 1,333 / 2 = 0,667 ) = b / v ( = 3,333 / 5 = 0,667 ) !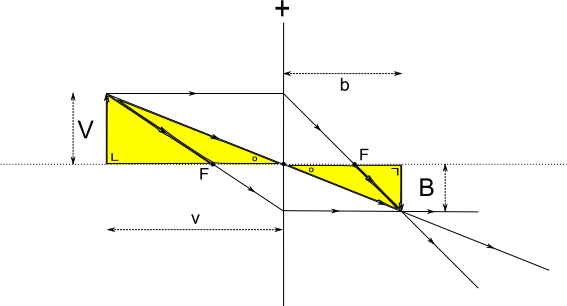




Nu kunnen we de tabel gaan maken. We vullen nu alle waarden in voor alle voorwerpsafstanden, die we al getekend hebben.

v
(cm)		 b
(cm)		 f
(cm)		 V
(cm)		 B
(cm)		 N=B/V
(-)		 N=b/v
(-)		 vergroot/
even groot/
verkleind		 reëel/
virtueel
6 3 2 2 1 N=1/2=
0,5		 N=3/6=
0,5		 verkleind reëel
5 3,333 2 2 1,333 N=1,333/2=
0,667		 N=3,333/5=
0,667		 verkleind reëel
4 4 2 2 2 N=2/2=
1		 N=4/4=
1		 even groot reëel
3 6 2 2 4 N=4/2=
2		 N=6/3=
2		 vergroot reëel
2 ∞ 2 2 ∞ N=∞/2=
∞		 N=∞/2=
∞		 geen beeld geen beeld
1,5 -6 2 2 -8 N=-8/2=
-4		 N=-6/1,5=
-4		 vergroot virtueel
1 -2 2 2 -4 N=-4/2=
-2		 N=-2/1=
-2		 vergroot virtueel
0,5 -0,667 2 2 -2,667 N=-2,667/2=
-1,333		 N=-0,667/0,5=
-1,333		 vergroot virtueel

We merken op dat er bij v = 4 cm en v = 2 cm duidelijke veranderingen in de tabel te zien zijn. Dit is precies 2 keer de brandpuntsafstand en de brandpuntsafstand zelf !
De verandering bij v = 4 cm = 2f gaat van verkleind naar vergroot (het beeld blijft gewoon reëel).
De verandering bij v = 2 cm = f gaat van reëel naar virtueel (het beeld blijft vergroot).
We maken de tabel wat algemener:

v b N vergroot/
even groot/
verkleind		 reëel/
virtueel
2f<v f<b<2f N<1 verkleind reëel
v=2f b=2f N=1 even groot reëel
f<v<2f 2f<b N>1 vergroot reëel
v=f ∞ N=∞ geen beeld geen beeld
v<f b<-v N<-1 vergroot virtueel

Met behulp van deze tabel kunnen we voorspellen, hoe het beeld eruit zal gaan zien. We kiezen eens f = 3 cm en v = 7 cm.
Volgens de tabel moet het beeld verkleind zijn en reëel (v>2f want 7>2*3=6)). Probeer dit eens te tekenen en te zien of dat waar is of niet !
Hoe zal het beeld eruit zien bij f = 3 cm en v = 4 cm ?



We kunnen nu voorspellen hoe het beeld eruit ziet bij verschillende voorwerpsafstanden ten opzichte van de brandpuntsafstand.
Kunnen we de beeldshoogte en de beeldsafstand ook precies berekenen ? Dat gaan we nu bekijken.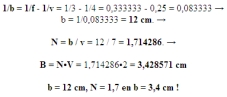


Berekening.