          |
Als je de samenvatting nog een keer wilt bekijken, kun je hier klikken:
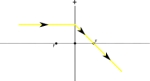
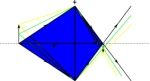
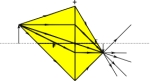
Samenvatting Berekenen beeldReken alle berekeningen zelf na en schrijf ze over ! Begrijp elke stap die gezet wordt !In het vorige gedeelte hebben we met behulp van een gelijkvormige driehoek gezien dat geldt: N = B / V = b / v. In de tekening zijn nog 2 gelijkvormige driehoeken te vinden. (Zie tekening)  De verhoudingen tussen deze 2 driehoeken is weer de vergroting, want de zijden B en V zitten weer in beide driehoeken. Er geldt dus zelfs: N = B / V = b / v = f / (v-f). Als we b / v = f / (v-f) uitwerken krijgen we de lenzenwet: b / v = f / (v-f) → (kruislings vermenigvuldigen) b•(v-f) = v•f → (haakjes wegwerken) b•v - b•f = v•f → (elke term delen door b•v•f) b•v / (b•v•f) - b•f / (b•v•f) = v•f / (b•v•f) → (gelijke factoren boven en onder wegstrepen) 1/f - 1/v = 1/b → (1/v naar andere kant van het gelijkteken) 1/f = 1/v + 1/b (de lenzenwet) Met behulp van deze formule en de al bekende vergelijking N = B / V = b / v kunnen we voorspellen, hoe het beeld eruit zal gaan zien. We kiezen weer f = 3 cm en v = 7 cm. En we kiezen voor V = 2 cm. Volgens de tabel moet het beeld verkleind zijn en reëel (v>2f want 7>2*3=6)) en dit kwam ook uit de tekening. Hoe berekenen we dat nou ? 1/f = 1/v + 1/b schrijven we eerst om, zodat we b makkelijker kunnen berekenen en dan vullen we de gegevens in: 1/f = 1/v + 1/b → (1/v naar de andere kant van het gelijkteken) 1/f - 1/v = 1/b → (links en rechts even verwisselen) 1/b = 1/f - 1/v = 1/3 - 1/7 = 0,333333 - 0,142857 = 0,190476 → (1/b is dit getal dus b = 1/getal) b = 1/0,190476 = 5,25 cm. → (nu kunnen we de vergroting berekenen) N = b / v = 5,25 / 7 = 0,75. → (nu kunnen we de beeldshoogte berekenen (V=2 cm) ) N = B / V schrijven we weer even om, zodat we B makkelijker kunnen berekenen en dan vullen we N en V in: B = N•V = 0,75•2 = 1,5 cm b = 5,25 cm, N = 0,75 en B = 1,5 cm ! We weten dus precies waar het snijpunt achter de lens moet komen ! En we zien dat inderdaad het beeld verkleind is (N = 0,75) en reëel (b > 0) ! We doen er nog één en kiezen f = 3 cm, v = 4 cm en V = 2 cm. Volgens de tabel moet het beeld vergroot zijn en reëel (f<v<2f want 3<4<6)). Een korter opgeschreven berekening: 1/b = 1/f - 1/v = 1/3 - 1/4 = 0,333333 - 0,25 = 0,083333 → b = 1/0,083333 = 12 cm. → N = b / v = 12 / 7 = 1,714286. → B = N•V = 1,714286•2 = 3,428571 cm b = 12 cm, N = 1,7 en B = 3,4 cm ! We zien dat inderdaad het beeld vergroot is (N = 1,7) en reëel (b > 0) ! We kunnen nu berekenen waar het beeld terecht komt bij verschillende voorwerpsafstanden ten opzichte van de brandpuntsafstand. Nu zijn we klaar om flink te oefenen ! Oefenen berekeningen met f, v, b, V, B en N. |
          |